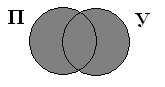Формы и законы мышления

В мышлении жизни сила,

Дыхание и свет.

Без мысли – мрак могилы, 

И жизни нет.  (В.Блейк)

Логика – наука, изучающая формы и законы мышления. (греч. "logos" - мысль, разум).

Историческая справка. Этапы развития логики.

1 этап - формальная логика. Основатель – Аристотель (384-322 гг.до н.э.), ввел основные формы абстрактного мышления.

2 этап – математическая логика. Основатель – немецкий ученый и философ Лейбниц (1642-1716), предпринял попытку логических вычислений.

3 этап – математическая логика (булева алгебра). Основатель – английский математик Джордж Буль (1815-1864), ввел алфавит, орфографию и грамматику для математической логики.

До 20-х годов ХХ века логика развивалась в направлении формализации и каталогизации правильных способов рассуждений.

Классическая (двузначная) логика – это первая ступень развития формальной логики.

Вторая ступень – символическая (математическая) систематизирует формы мышления, применяя математические методы и специальный аппарат символов. Исследует содержательное мышление с помощью исчислений.

Алгебра логики (булева алгебра, алгебра высказываний)– это математический аппарат, с помощью которого записывают (кодируют), упрощают, вычисляют и преобразовывают логические высказывания.

Математическая логика - система обозначений и правил, применимая ко всевозможным объектам, от чисел до предложений, и позволяющая закодировать высказывания с помощью символов своего языка, а затем манипулировать ими.

Логические функции, законы и тождества алгебры логики

Содержательные логические задачи

Содержательные логические задачи очень интересны, увлекательны и являются хорошей тренировкой мыслительной активности. Методов решения задач много: таблицы истинности, подтверждение или опровержение гипотезы, построение таблиц, построение и преобразование логических функций, построение логических цепочек, диаграммы Венна, с помощью графов и др.
Предлагаю вам попробовать свои силы и решить задачи любым, удобным для вас способом.
Выбирайте любой. 
Оформившие решение 5 любых задач, получат оценку.

Перейти к задачам...

№2. Умение определять значение логического выражения

2.  Умение определять значение логического выражения

Справка

Условные обозначения логических операций

¬ A,                      не A (отрицание, инверсия)

A Ù B, A & B             A и B (логическое умножение, конъюнкция)

A Ú B,              A или B (логическое сложение, дизъюнкция)

Приоритет логических операций (порядок выполнения):

1)    отрицание НЕ, 2) умножение И, 3) сложение ИЛИ.

Таблицы истинностей

0 – ложь, 1 - истина А не А 0 1 1 0

А В А и В А или В 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 1

Пример

Для какого из указанных значений числа Х истинно выражение (X>2) & ¬(X>3)?

1)    1

2)    2

3)    3

4)    4

Решение.

Подставляем каждое из чисел и поверяем истинность выражения:

1) (1>2) &¬(1>3) = ложь & ¬ложь =  ложь & истина = ложь

2) (2>2) & ¬(2>3) = Л & ¬Л =  Л & И = Л

3) (3>2) & ¬(3>3) = И & ¬Л =  И & И = И

3) (4>2) & ¬(4>3) = И & ¬И =  И & Л = Л

Ответ: 3.

Задачи

1. Для какого из указанных значений числа Х истинно выражение (X<3) & ((X<2) V (X>2))?

1)    1

2)    2

3)    3

4)    4

2. Для какого из указанных значений числа X ложно выражение (X > 2) ИЛИ НЕ (X > 1)?

1)    1

2)    2

3)    3

4)    4

3. Для какого из указанных значений X истинно высказывание ((X<5) ∨ ((X>5)) ∧ (X>15))?

1)    1

2)    5

3)    10

4)    15

4. Для какого из указанных значений числа Х истинно выражение (X>1) & (X>2) & (X≠3)?

1)    1

2)    2

3)    3

4)    4

5. Для какого из приведенных чисел истинно высказывание: НЕ(Первая цифра четная) И НЕ(Вторая  цифра нечетная)?

1)    4562

2)    6843

3)    3561

4)    1234

6. Для какого из приведенных слов истинно логическое выражение   НЕ(первая буква гласная) И НЕ (третья буква согласная)?

1)    модем

2)    адрес

3)    связь

4)    канал

7. Для какого из приведенных имен истинно высказывание: ￢ (первая буква согласная ∧ вторая буква гласная)∧ (последняя буква гласная)

1)    СОФИЯ

2)    АРКАДИЙ

3)    СВЕТЛАНА

4)    МАРИНА

8. Для какого из приведенных имен истинно высказывание: (последняя буква согласная) И НЕ ((первая буква гласная) И (вторая буква согласная))

1)    ПАВЕЛ

2)    АРКАДИЙ

3)    АНТОН

4)    ЕМЕЛЯ

Решение содержательных логических задач с помощью кругов Эйлера/диаграмм Венна

Математическая справка. Диаграммы Эйлера-Венна используются прежде всего в теории множеств как схематичное изображение всех возможных пересечений нескольких множеств. В общем случае они изображают все 2n комбинаций n свойств.

Смысл логических связок становится более понятным, если проиллюстрировать их с помощью графической схемы – кругов Эйлера (диаграмм Эйлера-Венна).

Логическая связка	Пример	Пояснение	Круги Эйлера
& - “И” (пересечение множеств)	Бабочки & Мадагаскар	Результат операции "И": множество, включающее в себя только бабочек, обитающих на острове Мадагаскар	Рис.1
| - “ИЛИ” (объединение множеств)	Бабочки | Мадагаскар	Результат операции "ИЛИ": множество всех бабочек и бабочек Мадагаскара	Рис.2

Тест "Логические функции"

Диаграммы Венна

Упростите логические выражения

Домашнее задание по теме "Законы и тождества алгебры логики"

1. Упростить выражения:

•     1) не(не А или В или С) или А и не (В и С)
•     2). не(А и В или не (А и В)) и не( не А и не В или А и не В)
•     3). (А либо В) и (В либо С)

2.  Определить, на каких наборах логических переменных, функция принимает значение "истина" (построить таблицу истинности). Ответ записываем в следующем формате, например, (0, 0, 0), (0, 1, 1).

F(x, y, z) = (xy + xz + yz) х

Постройте таблицы истинности - тренинг

Отношения между понятиями

Домашнее задание:
1. Прочитать теоретический материал.
2. Электронная тетрадь Отношения между понятиями, множествами
3. Являются ли следующие понятия совместимыми: 

• а) монитор, клавиатура; 
• б) принтер,  проектор;
• в) черный квадрат, красный квадрат;
• г) лейтенант, старший лейтенант;
• д) хищник, лев; 
• е) Европа, Азия?

4. Определите вид отношения между следующими понятиями и изобразите его с помощью кругов Эйлера: 

• а)  школа, образовательное учреждение; 
• б) Ю. Гагарин; первый человек, полетевший в космос;
• в) русский писатель, автор поэмы "Мертвые души", писатель;
• г) президент, президент России, глава государства;
• д) художественная литература, литература, драматургия;
• е) отец, сын, мужчина, дедушка.

5. Определите вид отношений между понятиями, изобразите его с помощью круговых схем: 

• а) А — ученый, В — писатель, С — общественный деятель;
• б) А — участник отечественной войны 1812 года, В — генерал, С — гусар; 
• в) А — автор романа "Мастер и Маргарита", В — писатель, С — русский писатель;
• д) А — еженедельник, В — периодическое издание, С — газета "Ведомости".

Для определения вида отношений между понятиями по объему нужно: 

1) соотнести представление об объеме понятия с кругами Эйлера; 

2) если дано несколько понятий, определить сначала отношение между двумя, а затем присоединять по-одному остальные.

Пример: А — наука, В — информатика, С — школьная информатика. Школьная информатика является разделом общей информатики, но только некоторые разделы общей информатики входят в курс школьной, следовательно, между понятиями  "информатика" и "школьная информатика" существует отношение вида   и рода, т.е. круг С входит полностью в круг В. Такое же отношение между понятиями "наука" и "информатика", значит круг В  входит в круг А.
Таким образом, все понятия в задаче являются совместимыми: отношение подчинения между А и В, А и С, В и С.

Сложные высказывания

Высказывание - это форма мышления, выраженная повествовательным предложением, в которой что-либо утверждается или отрицается об объектах, их свойствах или отношениях.

ПРОСТОЕ  высказывание (логическая переменная)  - высказывание, в котором ни одна  его часть сама не является высказыванием.

СЛОЖНОЕ высказывание (логическая функция). Состоит из нескольких простых высказываний, соединенных между собой с помощью логических операций

Мы часто используем сложные высказывания в речи, например:

• В портфеле ученика лежат учебники, тетрадки и ручки.
• Если завтра будет дождь, то мы с папой не поедем в лес.
• В нашем классе ребята занимаются плаванием или атлетикой.

Какие связки мы используем при построении сложных высказываний?

Основные операции булевой алгебры

• Конъюнкция – И, логическое умножение.
• Дизъюнкция – ИЛИ, логическое сложение
• Отрицание   - НЕ
• Импликация – логическое следование
• Эквиваленция – логическое тождество

Любое сложное высказывание можно записать с помощью основных логических операций И, ИЛИ, НЕ.

Порядок выполнения логических операций

 1) операции в скобках;

 2) отрицание;

 3) логическое умножение;

 4) логическое сложение;

 5) импликация;

 6) эквиваленция.

Формы и законы мышления

Скульптура головы Аристотеля

1. Выучить определения

• Формы и законы мышления

2. Ответить на вопрос письменно в тетрадях: 

• как  и в каких сферах применяются законы логики в информатике.

Способы решения содержательных логических задач

Отношения между понятиями

Понятие - это форма мышления, в которой отражаются существенные признаки одноэлементного класса или класса однородных предметов.

Всякое понятие имеет содержание и объем. Содержанием понятия называется совокупность существенных признаков одноэлементного класса или класса однородных предметов, отраженных в этом понятии. Содержанием понятия “квадрат” является совокупность двух существенных признаков: “быть прямоугольником” и “иметь равные стороны”.

Объемом понятия называют совокупность (класс) предме­тов, которая мыслится в понятии. Объективно, т. е. вне созна­ния человека, существуют различные предметы, например, школьники. Под объемом понятия “школьник” подразумевает­ся множество всех школьников, которые существуют сейчас, су­ществовали ранее и будут существовать в будущем. Класс (или множество) состоит из отдельных объектов, которые называ­ются его элементами. В зависимости от их числа множества делятся на конечные и бесконечные. Например, множество сто­лиц государств конечно, а множество натуральных чисел беско­нечно. Множество (класс) А называется подмножеством (под­классом) множества (класса) В, если каждый элемент А является элементом В. Такое отношение между подмножеством А и множеством В называется отношением включения класса А в класс В и записывается так: А c В. Читается: класс А входит в класс В. Это отношение вида и рода (например, класс “стол” входит в класс “мебель”).

Отношение принадлежности элемента а классу А записыва­ется так: а є А. Читается: элемент а принадлежит классу А. Например, а - “Нева” и А - “река”.

Классы А и В являются тождественными (совпадающими), если А c В и В c А, что записывается как А=В.

Закон обратного отношения между объемами и содержаниями понятий

В этом законе речь идет о понятиях, находящихся в родо­видовых отношениях. Объем одного понятия может входить в объем другого понятия и составлять при этом лишь его часть. Например, объем понятия “хищная рыба” целиком входит в объ­ем другого, более широкого по объему понятия “рыба” (состав­ляет часть объема понятия “рыба”). При этом содержание пер­вого понятия оказывается шире, богаче (содержит больше при­знаков), чем содержание второго. 

На основе обобщения такого рода примеров можно сформулировать следующий закон: чем шире объем понятия, тем уже его содержание, и наоборот. Этот закон называется законом обратного отношения между объе­мом и содержанием понятия. Он указывает на то, что чем меньше информации о предметах, заключенной в понятии, тем шире класс предметов и неопределеннее его состав (например, “водопад”), и наоборот, чем больше информации в понятии (например, “крупный водопад” или “крупный водопад в Канаде”), тем уже и определеннее круг его предметов, или даже мыслится только один предмет.

Предметы мира находятся друг с другом во взаимосвязи и взаимообусловленности. Поэтому и понятия, отражающие эти предметы, также находятся в определенных отношениях. Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми (например, “поэма” и “колодец”; “невоспитанность” и “радуга”), остальные понятия называются сравнимыми.

Сравнимые понятия делятся по объему на совместимые (объемы этих понятий совпадают полностью или частично) и несовместимые (их объемы не имеют общих элементов).

Типы совместимости:

равнозначность (тождество), перекрещивание,

подчинение (отношение рода и вида)

Отношения между понятиями изображают с помощью круговых схем (кругов Эйлера)', где каждый круг обозначает объем понятия. Кругом изображается и единичное понятие.